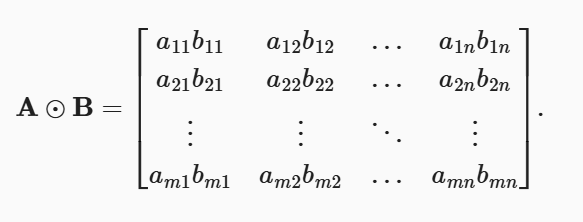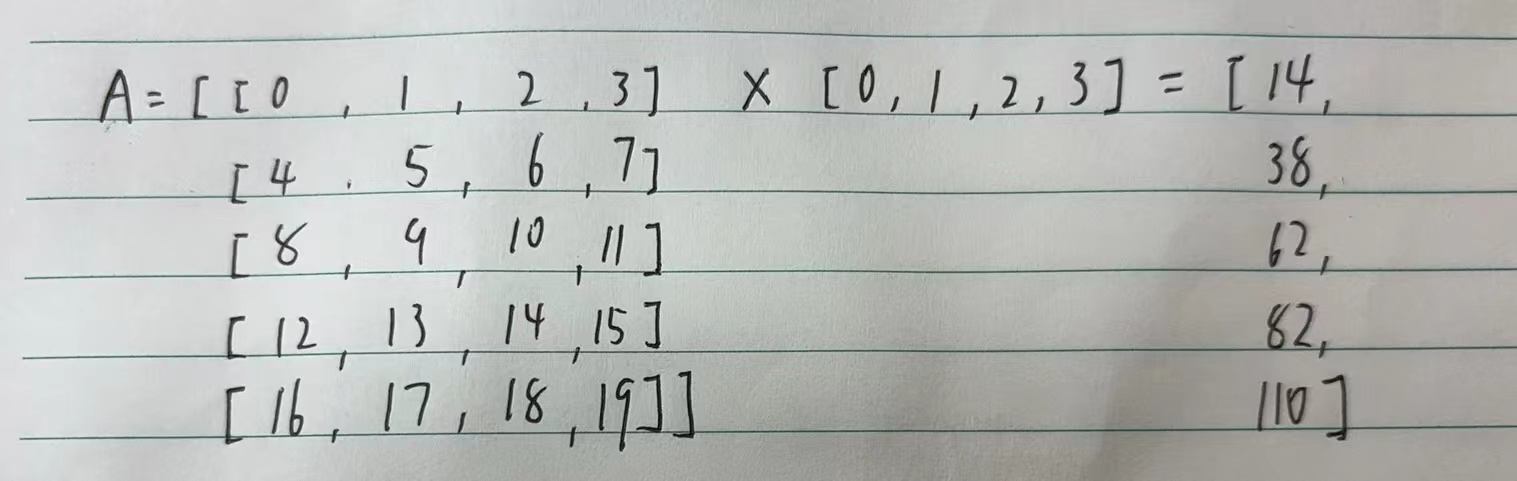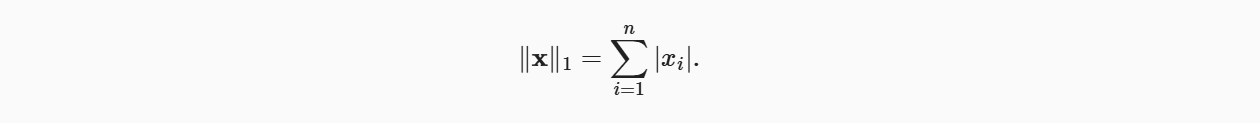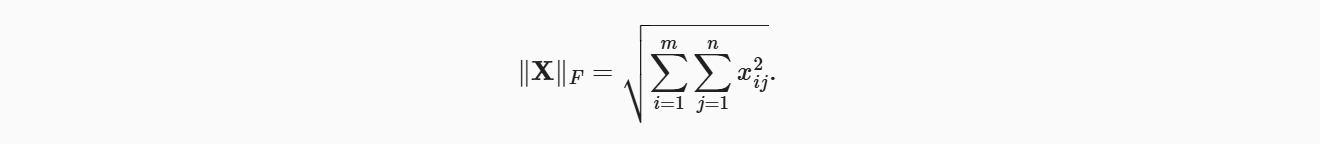Pytorch1线性代数实现
Pytorch learning notes1 –线性代数实现
矩阵
正如向量将标量从零阶推广到一阶,矩阵将向量从一阶推广到二阶。 矩阵,我们通常用粗体、大写字母来表示 (例如,𝑋、𝑌和𝑍), 在代码中表示为具有两个轴的张量。
数学表示法使用𝐴∈𝑅𝑚×𝑛 来表示矩阵𝐴,其由𝑚行和𝑛列的实值标量组成。 我们可以将任意矩阵𝐴∈𝑅𝑚×𝑛视为一个表格, 其中每个元素𝑎𝑖𝑗属于第𝑖行第𝑗列:
创建矩阵
当调用函数来实例化张量时, 我们可以通过指定两个分量𝑚和𝑛来创建一个形状为𝑚×𝑛的矩阵。
1 | A = torch.arange(20).reshape(5, 4) |
1 | tensor([[ 0, 1, 2, 3], |
矩形转置
1 | A.T |
1 | tensor([[ 0, 4, 8, 12, 16], |
张量
就像向量是标量的推广,矩阵是向量的推广一样,我们可以构建具有更多轴的数据结构。 张量(本小节中的“张量”指代数对象)是描述具有任意数量轴的𝑛维数组的通用方法。 例如,向量是一阶张量,矩阵是二阶张量。 张量用特殊字体的大写字母表示(例如,𝑋、𝑌和𝑍), 它们的索引机制(例如𝑥𝑖𝑗𝑘和[𝑋]1,2𝑖−1,3)与矩阵类似。
当我们开始处理图像时,张量将变得更加重要,图像以𝑛维数组形式出现, 其中3个轴对应于高度、宽度,以及一个通道(channel)轴, 用于表示颜色通道(红色、绿色和蓝色)。 现在先将高阶张量暂放一边,而是专注学习其基础知识。
1 | X = torch.arange(24).reshape(2, 3, 4) |
1 | tensor([[[ 0, 1, 2, 3], |
张量算法的基本性质
标量、向量、矩阵和任意数量轴的张量(本小节中的“张量”指代数对象)有一些实用的属性。 例如,从按元素操作的定义中可以注意到,任何按元素的一元运算都不会改变其操作数的形状。 同样,给定具有相同形状的任意两个张量,任何按元素二元运算的结果都将是相同形状的张量。 例如,将两个相同形状的矩阵相加,会在这两个矩阵上执行元素加法。
1 | A = torch.arange(20, dtype=torch.float32).reshape(5, 4) |
1 | (tensor([[ 0., 1., 2., 3.], |
具体而言,两个矩阵的按元素乘法称为Hadamard(哈达码)积(Hadamard product)(数学符号⊙)。 对于矩阵𝐵∈𝑅𝑚×𝑛, 其中第𝑖行和第𝑗列的元素是𝑏𝑖𝑗。 矩阵𝐴和𝐵的Hadamard积为:
1 | A * B |
1 | tensor([[ 0., 1., 4., 9.], |
将张量乘以或加上一个标量不会改变张量的形状,其中张量的每个元素都将与标量相加或相乘。
1 | a = 2 |
1 | (tensor([[[ 2, 3, 4, 5], |
降维
我们可以对任意张量进行的一个有用的操作是计算其元素的和。 数学表示法使用∑符号表示求和。 为了表示长度为𝑑的向量中元素的总和,可以记为∑𝑖=1𝑑𝑥𝑖。 在代码中可以调用计算求和的函数:
1 | x = torch.arange(4, dtype=torch.float32) |
1 | (tensor([0., 1., 2., 3.]), tensor(6.)) |
我们可以表示任意形状张量的元素和。 例如,矩阵𝐴中元素的和可以记为∑𝑖=1𝑚∑𝑗=1𝑛𝑎𝑖𝑗。
1 | A.shape, A.sum() |
1 | (torch.Size([5, 4]), tensor(190.)) |
默认情况下,调用求和函数会沿所有的轴降低张量的维度,使它变为一个标量。 我们还可以指定张量沿哪一个轴来通过求和降低维度。 以矩阵为例,为了通过求和所有行的元素来降维(轴0),可以在调用函数时指定axis=0。 由于输入矩阵沿0轴降维以生成输出向量,因此输入轴0的维数在输出形状中消失。
1 | A_sum_axis0 = A.sum(axis=0) #行,求完后只剩下一行 |
1 | (tensor([40., 45., 50., 55.]), torch.Size([4])) |
指定axis=1将通过汇总所有列的元素降维(轴1)。因此,输入轴1的维数在输出形状中消失。
1 | A_sum_axis1 = A.sum(axis=1) #列,求完后只剩下一列 |
1 | (tensor([ 6., 22., 38., 54., 70.]), torch.Size([5])) |
沿着行和列对矩阵求和,等价于对矩阵的所有元素进行求和。
1 | A.sum(axis=[0, 1]) # 结果和A.sum()相同 |
一个与求和相关的量是平均值(mean或average)。 我们通过将总和除以元素总数来计算平均值。 在代码中,我们可以调用函数来计算任意形状张量的平均值。
1 | A.mean(), A.sum() / A.numel() |
1 | (tensor(9.5000), tensor(9.5000)) |
同样,计算平均值的函数也可以沿指定轴降低张量的维度。
非降维求和
有时在调用函数来计算总和或均值时保持轴数不变会很有用。
1 | sum_A = A.sum(axis=1, keepdims=True) |
1 | tensor([[ 6.], |
如果我们想沿某个轴计算A元素的累积总和, 比如axis=0(按行计算),可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。
1 | A.cumsum(axis=0) |
1 | tensor([[ 0., 1., 2., 3.], |
点积(Dot Product)
我们已经学习了按元素操作、求和及平均值。 另一个最基本的操作之一是点积。 给定两个向量𝑥,𝑦∈𝑅𝑑, 它们的点积(dot product)𝑥⊤𝑦 (或⟨𝑥,𝑦⟩) 是相同位置的按元素乘积的和:𝑥⊤𝑦=∑𝑖=1𝑑𝑥𝑖𝑦𝑖。
1 | y = torch.ones(4, dtype = torch.float32) |
1 | (tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.)) |
我们也可以通过执行按元素乘法,然后进行求和来表示两个向量的点积:
1 | torch.sum(x * y) |
1 | tensor(6.) |
点积在很多场合都很有用。 例如,给定一组由向量𝑥∈𝑅𝑑表示的值, 和一组由𝑤∈𝑅𝑑表示的权重。 𝑥中的值根据权重𝑤的加权和, 可以表示为点积𝑥⊤𝑤。 当权重为非负数且和为1(即(∑𝑖=1𝑑𝑤𝑖=1))时, 点积表示加权平均(weighted average)。 将两个向量规范化得到单位长度后,点积表示它们夹角的余弦
矩阵-向量积
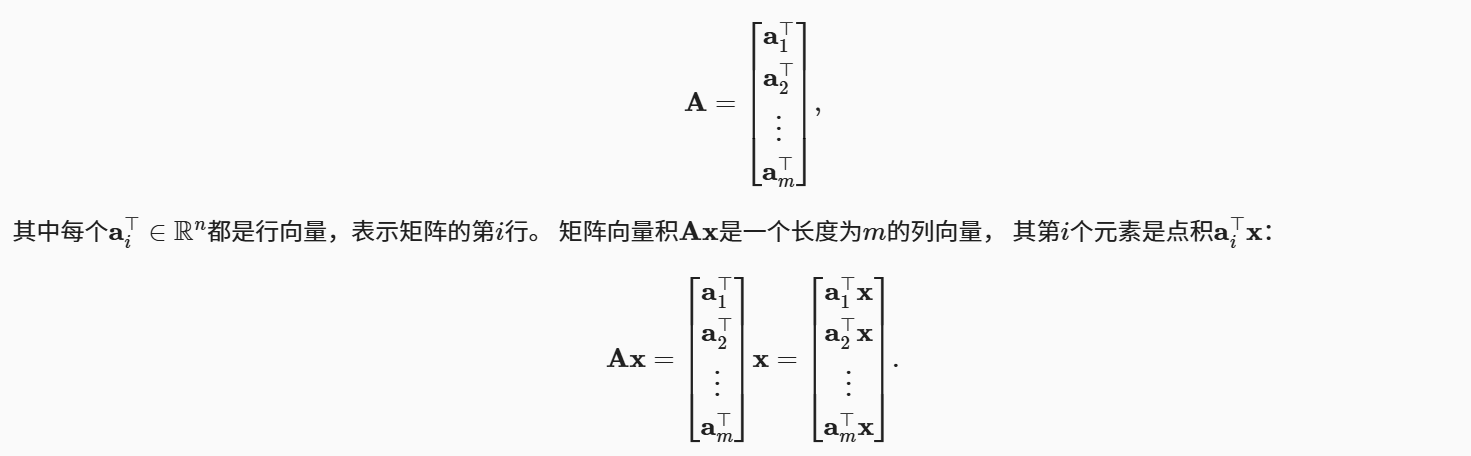
回顾矩阵𝐴∈𝑅𝑚×𝑛和向量𝑥∈𝑅𝑛。 让我们将矩阵𝐴用它的行向量表示:
我们可以把一个矩阵𝐴∈𝑅𝑚×𝑛乘法看作一个从𝑅𝑛到𝑅𝑚向量的转换。 这些转换是非常有用的,例如可以用方阵的乘法来表示旋转。 后续章节将讲到,我们也可以使用矩阵-向量积来描述在给定前一层的值时, 求解神经网络每一层所需的复杂计算。
在代码中使用张量表示矩阵-向量积,我们使用**mv函数。 当我们为矩阵A和向量x调用torch.mv(A, x)时,会执行矩阵-向量积。 注意,A的列维数(沿轴1的长度)必须与x的维数(其长度)相同**。
1 | A.shape, x.shape, torch.mv(A, x) |
1 | (torch.Size([5, 4]), torch.Size([4]), tensor([ 14., 38., 62., 86., 110.])) |
图片解释:
矩阵-矩阵乘法
假设有两个矩阵𝐴∈𝑅𝑛×𝑘和𝐵∈𝑅𝑘×𝑚
我们可以将矩阵-矩阵乘法AB看作简单地执行𝑚次矩阵-向量积,并将结果拼接在一起,形成一个𝑛×𝑚矩阵。 在下面的代码中,我们在A和B上执行矩阵乘法。 这里的A是一个5行4列的矩阵,B是一个4行3列的矩阵。 两者相乘后,我们得到了一个5行3列的矩阵。
1 | B = torch.ones(4, 3) |
1 | tensor([[ 6., 6., 6.], |
矩阵-矩阵乘法可以简单地称为矩阵乘法,不应与“Hadamard积”混淆
范数
性代数中最有用的一些运算符是范数(norm)。 非正式地说,向量的范数是表示一个向量有多大。 这里考虑的大小(size)概念不涉及维度,而是分量的大小。
在线性代数中,向量范数是将向量映射到标量的函数𝑓。 给定任意向量𝑥,向量范数要满足一些属性。 第一个性质是:如果我们按常数因子𝛼缩放向量的所有元素, 其范数也会按相同常数因子的绝对值缩放:
𝑓(𝛼𝑥)=|𝛼|𝑓(𝑥).
第二个性质是熟悉的三角不等式:
𝑓(𝑥+𝑦)≤𝑓(𝑥)+𝑓(𝑦).
第三个性质简单地说范数必须是非负的:
𝑓(𝑥)≥0.
这是有道理的。因为在大多数情况下,任何东西的最小的大小是0。 最后一个性质要求范数最小为0,当且仅当向量全由0组成。
∀𝑖,[𝑥]𝑖=0⇔𝑓(𝑥)=0.
范数听起来很像距离的度量。 欧几里得距离和毕达哥拉斯定理中的非负性概念和三角不等式可能会给出一些启发。 事实上,欧几里得距离是一个𝐿2范数: 假设𝑛维向量𝑥中的元素是𝑥1,…,𝑥𝑛,其𝐿2范数是向量元素平方和的平方根:
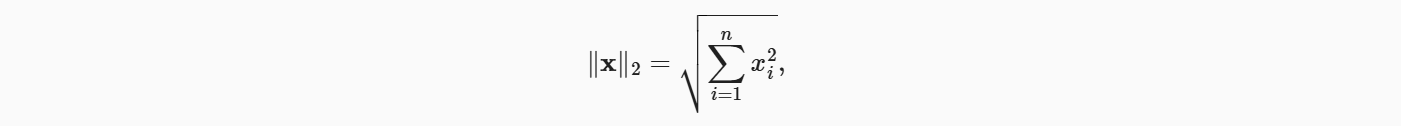
其中,在𝐿2范数中常常省略下标2,也就是说‖𝑥‖等同于‖𝑥‖2。 在代码中,我们可以按如下方式计算向量的𝐿2范数。
1 | u = torch.tensor([3.0, -4.0]) |
1 | tensor(5.) |
深度学习中更经常地使用𝐿2范数的平方,也会经常遇到𝐿1范数,它表示为向量元素的绝对值之和:
与𝐿2范数相比,𝐿1范数受异常值的影响较小。 为了计算𝐿1范数,我们将绝对值函数和按元素求和组合起来。
1 | torch.abs(u).sum() |
1 | tensor(7.) |
类似于向量的𝐿2范数,矩阵𝑋∈𝑅𝑚×𝑛的Frobenius范数(Frobenius norm)是矩阵元素平方和的平方根:
Frobenius范数满足向量范数的所有性质,它就像是矩阵形向量的𝐿2范数。 调用以下函数将计算矩阵的Frobenius范数。
1 | torch.norm(torch.ones((4, 9))) |
1 | tensor(6.) |
——文章由沐神的教学文档改编